آموزش فرآیند تحلیل سلسله مراتبی-آموزش AHP
روش AHP توسط فردی به نام ساعتی Saaty در سال 1980 ارائه گردید. این روش یکی از جامع ترین مدل MADM به شمار می رود. از مزایای این روش می توان به موارد زیر اشاره نمود: امکان فرموله کردن مساله بصورت ساختار سلسله مراتبی چند سطحی را فراهم می کند. تطابق بالای این روش را با ذهن افراد نشان داده و مساله اصلی را با ساختار سلسله مراتبی به صورت ساده تر نشان می دهد. همچنین از آنجایی که این روش بر اساس مقایسه های زوجی بنا نهاده شده و امکان بررسی سناریوهای مختلف را به مدیران می دهد.
AHP بر اساس سه اصل زیر استوار است:
1) اصل ترسیم درخت سلسله مراتبی
2) اصل تدوین و تعیین اولویت ها
3) اصل سازگاری منطقی قضاوت ها
الف) اصل ترسیم درخت سلسله مراتبی
بر اساس این اصل، از آنجایی که درک و فهم یک مساله در حالت کلی برای انسان، کاری به مراتب پیچیده و دشوار است و ممکن است ابعاد مختلف و مهم یک مساله مورد توجه قرار نگیرد. از اینرو تجزیه یک مساله بزرگتر به عناصر کوچک تر، روابط و مفاهیم موجود در مساله تصمیم گیری و ارتباط بین هر عنصر با سایر عناصر، به دقت و سهولت قابل درک خواهد بود. با انجام این عمل، درخت ساختار سلسله مراتبی بوجود می آید که به درک و حل مساله کمک شایانی می نماید.
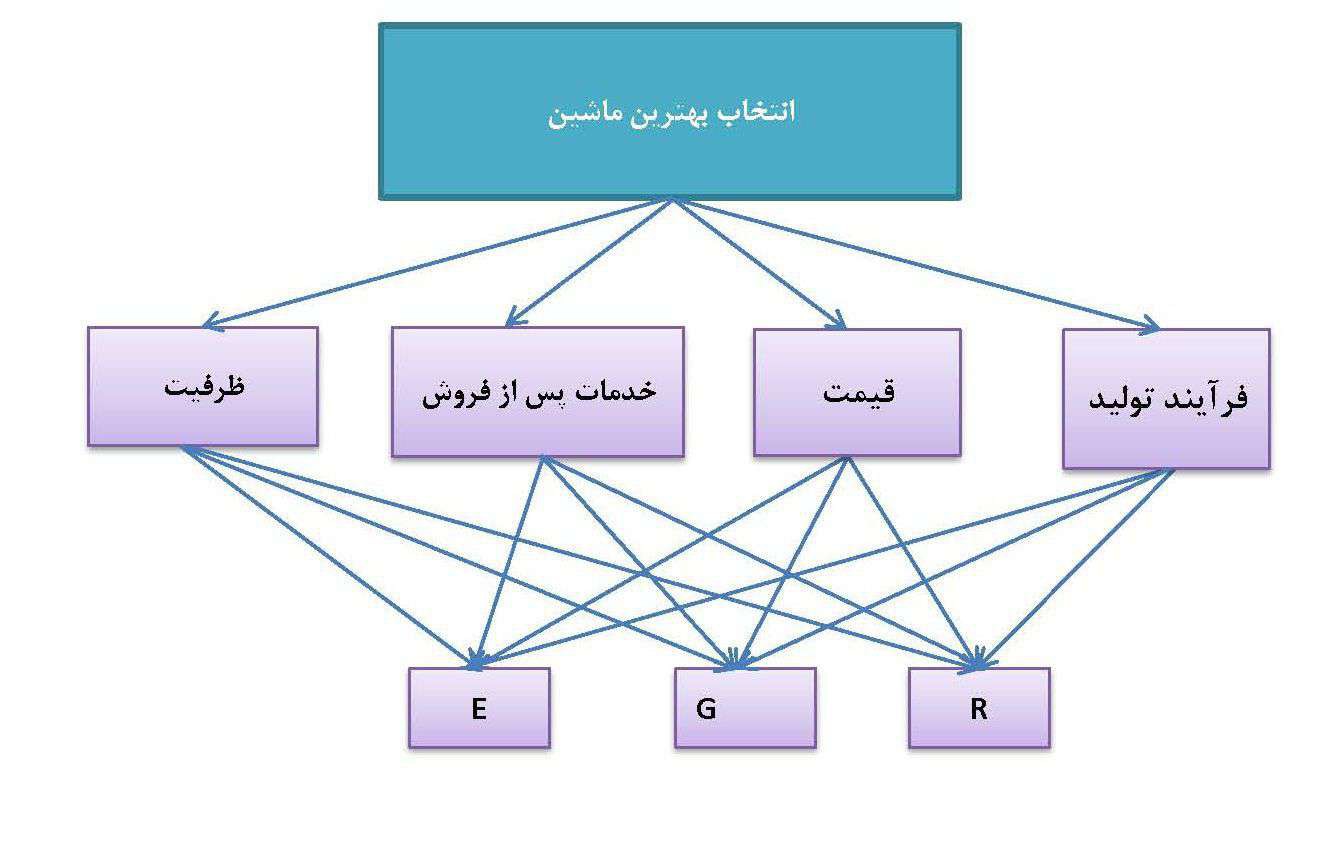
فرض کنید شرکتی می خواهد ماشینی را خریداری نمایید که سازندگان آن از سه کشور روسیه (R)، آلمان (G)، و انگلیس (E) هستند و برای این منظور چهار معیار ظرفیت، خدمات پس از فروش، قیمت و فرآیند تولید در نظر گرفته اند.
در درخت سلسله مراتبی، در سطح اول “هدف” (در این مساله انتخاب بهترین ماشین) قرار می گیرد. در سطح دوم معیارها ذکر می شوند (ممکن است در برخی از مسائل بیش از 3 سطح داشته باشیم یعنی برخی از معیارها شامل زیرمعیار باشند). در پایین ترین سطح، گزینه ها یا آلترناتیوها قرار می گیرند (در این مثال سطح 3) . برای این مساله ساختار سلسله مراتبی (درخت ساختار مساله) بصورت زیر رسم می شود.
 ب) تعیین اولویت ها
ب) تعیین اولویت ها
از آنجایی که انسان نمی تواند یک مساله را بطور کلی فهم و درک نماید، بنابراین مساله را به ساختار های کوچکتر تقسیم کرده و با توجه به معیارهای مشخص بین آنها مقایسات زوجی انجام می دهد. بنابراین روش AHP به جای ماتریس تصمیم (Decision matrix) که در روش هایی مانند TOPSIS استفاده می شود، از ماتریس مقایسات زوجی بهره می گیرد.
ج) سازگاری منطقی قصاوت ها
میزان ارتباط بین معیارهای مختلف در یک سطح از ساختار سلسله مراتبی را نشان می دهد. به عنوان مثال اگر معیار مورد نظر ما ظرفیت باشد، و اگر میزان اهمیت طرفیت نسبت به خدمات پس از فروش برای خبره 2 برابر باشد و میزان اهمیت خدمات پس از فروش نسبت به قیمت 3 برابر باشد، آنگاه میزان اهمیت طرفیت نسبت به قیمت 6 برابر خواهد بود. زمانی که تصمیم گیرنده پرسشنامه AHP (ماتریس مقایسه زوجی)را پر می کند قطعا خطا بوجود خواهد آمد و این خطا تا حدی قابل قبول است و اگر از حد خارج شد یا باید خبره تغییر کند یا مجدد از خبره نظر گرفته شود.
الگوریتم AHP
پس از گردآوری تمامی مقایسات زوجی لازم در تمامی سطوح، از گام های زیر برای انجام محاسبات AHP بهره می گیریم:
گام 1: تشکیل ماتریس مربعی بطوریکه سطرها و ستون ها همان معیارهای تصمیم گیری باشند
گام 2: از تصمیم گیرنده بخواهید معیارها را دو به دو با هم مقایسه کرده و میزان اهمیت هر یک را نسبت به معیار مقابل با استفاده از بازه عددی 1 تا 9 بیان نماید. بدیهی است که در این ماتریس قطر اصلی همواره برابر 1 بوده و مقادیر پایین قطر ماتریس معکوس مقادیر متناظر در بالای ماتریس خواهند بود.
گام 3: نرمال کردن ماتریس مقایسه زوجی (تقسیم هر عدد بر مجموع ستون خود)
گام 4: بدست اوردن میانگین مقایر هر سطر ماتریس نرمال شده در مرحله قبل (این عدد نشان دهنده وزن معیار مربوطه خواهد بود)
توضیحات: در روش های علمی روش بالا توصیه نمی شود. و روشهای بردار ویژه و یا روش حدقل مربعات توصیه می شود.
پس از این گام ها باید به سراغ نرخ سازگاری ماتریس مقایسه زوجی برویم.
محاسبه نرخ سازگاری در روش AHP
گام 1: محاسبه بردار مجموع وزنی (WSV): ماتریس مقایسات زوجی را در بردار وزن های نسبی بدست آمده ضرب کنید. به بردار حاصل، بردار مجموع وزنی گقته می شود.
گام 2: محاسبه بردار سازگاری: عناصر بردارمجموع وزنی را بر بردار وزن های نسبی تقسیم نمایید. به بردار حاصل، بردار سازگاری گفته می شود.
گام 3: محاسبه بزرگترین مقدار ویژه ی ماتریس مقایسات زوجی λmax: بزرگترین مقدار ویژه ماتریس مقایسات زوجی، میانگین عناصر بردار سازگاری است.
گام 4: محاسبه شاخص سازگاری (consistency index): شاخص سازگاری بصورت زیر محاسبه می شود:
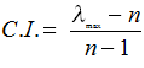 توصیحات: اکر ماتریس D (ماتریس مقایسات زوجی) را داشته باشیم می توان از خاصیت بردار ویژه (Eigen vector) برای محاسبه وزن و مقدار ویژه (Eigen value) برای شاخص سازگاری به صورت زیر بهره نمود.
توصیحات: اکر ماتریس D (ماتریس مقایسات زوجی) را داشته باشیم می توان از خاصیت بردار ویژه (Eigen vector) برای محاسبه وزن و مقدار ویژه (Eigen value) برای شاخص سازگاری به صورت زیر بهره نمود.
دترمینان ماتریس (D-λI) را محاسبه کرده و آن را مساوی صفر قرار داده و مقادیر λ را محاسبه کنید.
بزرگترین λ را λmax نامیده و آن را در رابطه
(D-λmax×I)W=0
قرار داده و با استفاده ازرابطه بالا مقادیر Wi ها (وزن ها) را محاسبه نمایید.
گام 5: محاسبه نرخ سازگاری: نرخ سازگاری بصورت زیر محاسبه می شود:
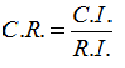 در فرمول بالا، شاخص تصادفی بصورت جدول زیر بدست می آید:
در فرمول بالا، شاخص تصادفی بصورت جدول زیر بدست می آید:
 در صورتی که نرخ سازگاری کمتر از 0.1 باشد ، ماتریس سازگار است و می توان به نتایج وزن ها اعتماد نمود. در غیر اینصورت DM یا تصمیم گیرنده باید در مقایسات زوجی تجدید نظر نماید.
در صورتی که نرخ سازگاری کمتر از 0.1 باشد ، ماتریس سازگار است و می توان به نتایج وزن ها اعتماد نمود. در غیر اینصورت DM یا تصمیم گیرنده باید در مقایسات زوجی تجدید نظر نماید.
لازم به ذکر است برای پر کردن ماتریس مقایسات زوجی از مقیاس 9 تایی ساعتی استفاده می شود تا اهمیت نسبی هر عنصر نسبت به سایر عناصر ماتریس مقایسات زوجی در رابطه با آن خصوصیت مشخص شود.
| ارزش | وضعيت مقايسه i نسبت به j | توضيح |
| ۱ | اهمیت يکسان Equally Preferred | دو عنصر اهمیت یکسانی دارند |
| ۳ | نسبتا مرجح Moderately Preferred | گزينه يا شاخص i نسبت به j كمي مهمتر است. |
| ۵ | ترجیح زیادStrongly Preferred | گزينه يا شاخص i نسبت به j مهمتر است. |
| ۷ | ترجیح بسیار زیاد Very strongly Preferred | گزينه i داراي ارجحيت خيلي بيشتري از j است. |
| ۹ | اهمیت مطلق Extremely Preferred | گزينه i از j مطلقاً مهمتر است و قابل مقایسه نیستند. |
| ۶-۴-۲ | ارزشهای بینابین در قضاوت ها | ارزشهاي بينابين را نشان ميدهد مثلا ۸، بيانگر اهميتي زيادتر از ۷ و پايينتر از ۹ براي i است. |
